​
Quickstart (10 minutes)

Welcome! In this Quickstart, we’ll guide you through building your first model in Dalus. We’re going to build a model of a satellite with 3 reaction wheels, design a simple attitude control system, and then verify a key performance parameter, settling_time, for that control system. Whether you’re new to system modeling or just getting started with Dalus, this hands-on example will help you get up to speed quickly and confidently.

​
Step 1: Create a New Model

Start by creating a new model in the Dalus dashboard. Give your model a descriptive name, such as “Satellite Quickstart”. This model is the isolated, collaborative environment that will contain your system’s requirements, architecture, and analysis all in one place. Creating a new model in Dalus

​
Step 2: Define Requirements

Satellites need to respond to new attitude commands from the ground promptly to face the necessary direction for imaging, telemetry, etc.. Let’s add a requirement that specifies the maximum allowable time to complete a commanded attitude maneuver:
Requirement: The Attitude Control and Determination Subsystem (ACDS) shall settle to within 0.1 degrees of the commanded attitude within 120 seconds after maneuver initiation.
Adding requirements in Dalus

​
Step 3: Build the Structure

Now let’s define the basic structure of our satellite. We’ll start by adding the main parts we’ll be focusing on for this quickstart:
  1. Add the Satellite as the root part of your model.
  2. Double-Click into the Satellite and add these subparts:
    • Reaction Wheels (x3): Add three reaction wheel components to represent the 3-axis control system.
    • Attitude Control & Determination System (ACDS): Add the Attitude Control and Determination Subsystem as a separate part.

​
Step 4: Add Part Attributes

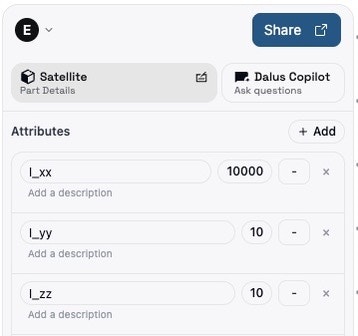
Now that we have the foundation, let’s assign some attributes. Attributes are values like “mass” or “moment of inertia” that describe a part’s physical properties and are accessible by any analysis we do. Add the satellite’s mass-moments of inertia as attributes in the Right Sidebar:
Attribute NameValueUnit
l_xx10kilogram meter squared
l_yy10kilogram meter squared
l_zz10kilogram meter squared
Adding attributes in Dalus

​
Step 5: Configure an Action (Analysis)

In this step, we’ll implement the action Point Satellite inside the Satellite part, which takes a commanded attitude and calculates how long it takes (among other things) to reach that attitude from its initial attitude (0,0,0).
  1. First, switch to the Action view in the Dalus interface. This will allow you to create and configure actions for your model, in this case, for the Satellite part.
  2. Add an action and name it “Point Satellite”.
  3. Double-click on the action and copy and paste this python code inside, which implements a simple Proportional-Derivative controller in 3 axes:
import numpy as np

# -- Satellite inertia (from attributes) --
I_xx = float(getAttribute(""))
I_yy = float(getAttribute(""))
I_zz = float(getAttribute(""))
I = np.array([I_xx, I_yy, I_zz])

# Control gains and limits
Kp = np.array([0.1, 0.1, 0.1])
Kd = np.array([1.5, 1.5, 1.5])
torque_cmd_max = 0.02

# Reaction wheel parameters
J_rw_x = 1.0  # example value, kg·m²
J_rw_y = 1.0  # example value, kg·m²
J_rw_z = 1.0  # example value, kg·m²
J_rw = np.array([J_rw_x, J_rw_y, J_rw_z])
efficiency = 0.9  # example value

# Initial attitude
a_x, a_y, a_z = 0, 0, 0  # deg
a_cmd_x, a_cmd_y, a_cmd_z = getInput("a_cmd_x"), getInput("a_cmd_y"), getInput("a_cmd_z")

attitude = np.deg2rad([a_x, a_y, a_z])
desired_attitude = np.deg2rad([a_cmd_x, a_cmd_y, a_cmd_z])

# Simulation settings
dt = 0.1
t_final = 200
times = np.arange(0, t_final, dt)

# Preallocate histories
error_norm = np.zeros_like(times)
torque_history = np.zeros((len(times), 3))
omega = np.zeros(3)
omega_rw = np.zeros(3)
power_history = np.zeros((len(times), 3))

# Initial error
prev_error = desired_attitude - attitude
initial_error_norm = np.linalg.norm(prev_error)
settling_time = None

settling_threshold = 0.1  # deg

# Simulation loop
for i, t in enumerate(times):
    error = desired_attitude - attitude
    error_dot = (error - prev_error) / dt
    prev_error = error

    # PD control and saturation
    torque_cmd = Kp * error + Kd * error_dot
    torque_cmd = np.clip(torque_cmd, -torque_cmd_max, torque_cmd_max)
    torque_history[i] = torque_cmd

    # Update satellite dynamics
    alpha = torque_cmd / I
    omega += alpha * dt
    attitude += omega * dt

    # Reaction wheel dynamics & power
    alpha_rw = torque_cmd / J_rw
    omega_rw += alpha_rw * dt
    power = np.abs(torque_cmd * omega_rw) / efficiency
    power_history[i] = power

    # Record error norm & settling time
    error_norm[i] = np.linalg.norm(error)
    if settling_time is None and np.rad2deg(error_norm[i]) < settling_threshold:
        settling_time = t

# Calculate rise time (10% to 90% of initial error)
e0 = initial_error_norm
rise_time = np.nan # Default to NaN

# Find indices where error crosses the thresholds
indices_start = np.where(error_norm <= 0.9 * e0)[0]
indices_end = np.where(error_norm <= 0.1 * e0)[0]

# Check if both thresholds were crossed
if len(indices_start) > 0 and len(indices_end) > 0:
    t_rise_start = times[indices_start[0]]
    t_rise_end = times[indices_end[0]]
    # Ensure start time is before end time (error is decreasing)
    if t_rise_end >= t_rise_start:
        rise_time = t_rise_end - t_rise_start
    else:
        # This case might happen if error oscillates around the threshold
        print("Warning: Could not determine a valid rise time (end time before start time).")

elif len(indices_start) == 0:
    print("Warning: Attitude error never reached 90% of the initial value.")
elif len(indices_end) == 0:
    print("Warning: Attitude error never reached 10% of the initial value.")


# Total energy consumed by wheels
total_power = np.sum(power_history, axis=1)
total_energy = np.trapz(total_power, times)  # Joules

# Results
print(f"Rise time: {rise_time:.1f} s" if not np.isnan(rise_time) else "Rise time: N/A (threshold not met)")
print(f"Settling time: {settling_time:.1f} s" if settling_time is not None else "Settling time: N/A (threshold not met)")
setAttribute("", settling_time if settling_time is not None else -1.0) # Use -1 or similar for unset value
# Set new attitude (for use in further analysis)
roll_deg, pitch_deg, yaw_deg = np.rad2deg(attitude)
print(f"Final attitude: roll={roll_deg:.2f} deg, pitch={pitch_deg:.2f} deg, yaw={yaw_deg:.2f} deg")
You’ll notice in the script, on line 23, we’re grabbing some input variables: a_cmd_x, a_cmd_y, and a_cmd_z. These need to be added to the action via the Right Sidebar. These are the commanded attitudes we are providing the script:
Input VariableValueUnit
a_cmd_x50deg
a_cmd_y50deg
a_cmd_z50deg
The controller will also use the I_xx, I_yy, and I_zz attributes you defined earlier. Copy their IDs from the Attributes dropdown and paste them in the getAttribute function’s argument. Finally, we need to set the settling_time; this is the key performance parameter we are evaluating. Go back to the Satellite part and add it as an attribute.
Attribute NameValueUnit
settling_time120s
Go back to the Point Satellite script and copy the attribute ID and paste it in setAttribute("", settling_time) between the "".
  • After running the simulation, the script will calculate the settling_time and set it for the Satellite’s attribute.

​
Step 6: Add a Requirement Constraint and Test

Now, let’s return to our requirements and add a constraint to the ACDS settling time requirement:
  1. Go to the requirements view and locate the ACDS settling time requirement.
  2. Click on its status, then under Add constraint, select the Attributes dropdown.
  3. Choose settling_time and set the limit to < 120 seconds.
  4. You’ll see the requirement status immediately update based on its current value.
Experiment a bit. Increase the moments of inertia (e.g., I_xx) in the Satellite’s attributes and re-run the simulation. Try to get the requirement to fail!

​
Step 7: Create a Simple State Machine

Next, let’s create a simple state machine to trigger our Point Satellite action instead of manually running it.
  1. Switch to the State view.
  2. Define two states: STANDBY and SURVEILLING.
  3. Connect them to add a transition between them. Name it anything.
  4. In the Point Satellite transition, select the Point Satellite action as an effect. This causes the action to execute whenever you transition from Standby to Surveilling.
  5. Use the states dropdown to first enter STANDBY. Then, switch to the Action view and transition to SURVEILLING to observe the effect taking place.
Although simple, this powerful principle can be used to orchestrate many actions for a complex state machine. Additional state machine features coming soon include:
  1. transition triggers - boolean expressions that automatically execute the transition if ALL evaluate to true.
  2. transition guards - boolean expressions that prevent the transition if ANY evaluate to true.

​
Next Steps

Ready to take your model to the next level? Here are a few ways you can extend and improve your satellite model:
  1. Parameterize Control Gains & Reaction Wheel Moments:
    • Add the proportional (Kp) and derivative (Kd) gains as attributes to the ACDS subsystem instead of hard-coding them in the Point Satellite script.
    • Similarly, add the Reaction Wheel moments (J_rw_x, J_rw_y, J_rw_z) as attributes of the Reaction Wheels .
    • Update the Point Satellite script to fetch these values using getAttribute. This is to organize your parameters logically, making them easy to find and tune as your model grows in complexity.
  2. Model Command Inputs from Ground Control:
    • Add a new part called Ground Control at the same level as the Satellite.
    • Connect the parts together to form an interface and add connections for a_cmd_x, a_cmd_y, and a_cmd_z instead of assigning them as inputs to the action.
    • In your script, use getConnection (passing in the ID) to access these command variables instead of getInput.
  3. Set and Reset the Satellite’s Current Attitude:
    • First, add attitude_x, attitude_y, and attitude_z as attributes to the Satellite part with initial values of 0.
    • Using the setAttribute(id, value) function, set the spacecraft’s attitude_x, attitude_y, attitude_z attributes in your script.
    • Run “Point Satellite” again and you should see them update!
    • Add a new action to “reset” the attitudes back to 0. Assign this action as an effect that triggers when entering the STANDBY state.
These improvements will make your model more realistic and modular. See if you can implement them—and experiment with different values and configurations to see how your system responds!